Despeje de literales en fórmulas de volumen

Una misma formula se puede expresar de distintas maneras, dependiendo de la variable que interesa calcular. 

La formula del volumen de prismas rectos rectangulares tiene cuatro variables: volumen (v), largo (l), ancho (a) y la altura (h).

Si se conocen tres valores, se puede conocer el cuarto valor con el despeje necesario:
para calcular la altura, para calcular el largo y para calcular el ancho.

Ahora considera la formula general del volumen de un prisma: área de la base por altura

Tomando en cuenta lo anterior, ¿cómo se calcula la altura del triangulo de la base de un prisma triangular?

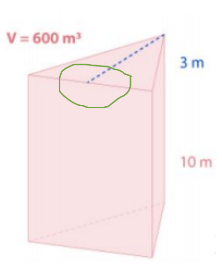
Simplemente es realizar las operaciones contrarias a las operaciones que tenemos en la formula, por ejemplo, si tenemos un prisma con un volumen de 600 centímetros cúbicos, con una altura del triangulo de 3 y una altura del prisma de 10 cm. Se empieza por dividir el volumen del prisma entre la altura, entonces tenemos 600 entre 10 y nos da 60, continuamos quitando el 2 y multiplicamos 60 por 2 que nos da 120, por ultimo dividimos 120 entre 3 y obtenemos 40, por lo tanto 40 es la medida de la altura del triangulo de la base del prisma.

 

PRACTICA:

Calcula los datos faltantes de los siguientes prismas.

1. Calcula la altura de un prisma rectangular cuyo largo mide 39 cm, ancho 16 cm y volumen de 14352 centímetros cúbicos.
2. Calcula el largo de prisma rectangular cuya altura es 20 cm, ancho 12 cm y volumen de 12000 centímetros cúbicos.
3. Calcula el volumen de un prisma octagonal de 4 dm de lado, apotema de 8 dm y altura de 15 dm.
4. Calcula el volumen de un prisma romboidal cuyas diagonales mayores y menores son 12 cm, 10 cm y que tiene una altura de 15 cm.