Sistemas de ecuaciones lineales 2 x 2, parte 1
En este primer acercamiento a los sistemas de ecuaciones se trata de conocer la definición de un sistema de ecuaciones así como utilizar procedimientos personales para encontrar los valores de las incógnitas.
Una pareja de ecuaciones lineales con dos incógnitas se llama sistema de ecuaciones lineales de 2 x 2, en las cuales cada incógnita se representa con diferente literal. En general un sistema de puede escribir:
donde "x" y "y" representan las incógnitas. Resolver el sistema es encontrar los valores para "x" y "y" que hagan verdaderas ambas ecuaciones.¿Como establecer un sistema de ecuaciones a partir de un problema?
Para entender la manera en establecer un sistema de ecuaciones a partir de un problema, veamos el siguiente ejemplo a partir de un problema:
Ejemplo 1: Gabriela compró, en alguna ocasión, 8 tortas y 5 jugos por los que pagó $152.00 y recuerda que las tortas cuestan $6.00 más que los jugos. ¿Qué pecio tiene una torta y un jugo?
primero, analizar sobre que situaciones se trata, es decir, los objetos o variables de las que habla el problema, en este caso es sobre tortas y jugos
Gabriela compró, en alguna ocasión, 8 tortas y 5 jugos por los que pagó $152.00 y recuerda que las tortas cuestan $6.00 más que los jugos. ¿Qué pecio tiene una torta y un jugo?
segundo, si ya conocemos las variables de las que trata el problema, se establece para cada uno alguna literal que represente dicha variable:
jugos ⇒ j
primero,encontrar las variables para posteriormente asignar la literal:
Un crucero tiene habitaciones dobles (2 camas) y sencillas (1 cama). En total tiene 47 habitaciones y 79 camas. ¿Cuántas habitaciones tiene cada piso?
segundo, asignamos literales a las variables encontradas (se puede asignar cualquier letra como literales):
habitaciones dobles ⇒ x
habitaciones sencillas ⇒ y
Resolución de sistema de ecuaciones
En este primer acercamiento la resolución de sistemas de ecuaciones será utilizando procedimientos personales o diversos, observa los siguientes ejemplos para entender la manera de resolver los ejercicios:
Ejemplo 1: Ernesto fue al cine con su familia. Compraron 5 boletos y 4 bolsas de palomitas y gastaron $250.00. Ernesto le preguntó a su papá por el precio de ambas cosas, a lo que el papá le respondió: "Las palomitas costarón $5.00 menos que cada boleto". ¿Qué precio tiene cada boleto y cada bolsa de palomitas?
Ejemplo 2: José Luis lleva en su cartera $1800.00 en billetes de $100.00 y $200.00. José Luis comentó que tenia 10 billetes. ¿Cuántos billetes de cada denominación lleva José Luis en la cartera?
1. Escribe un sistema de ecuaciones lineales para representar cada situación.
2. Aplica los procedimientos anteriores y resuelve los siguientes problemas:
- En un taller hay 15 vehículos entre coches y motocicletas; el número de llantas de todos los vehículos es de 48. ¿Cuántas motocicletas y coches hay?
- Juana fue al mercado y compró 3 kg de papas y 2 kg de jitomate. Si pagó $65.00 y el kilogramo de papas cuesta $15.00, ¿cuánto cuesta el kilogramo de jitomate?
- Si tres chocolates y un cuaderno costarón $50.00, ¿cuánto cuesta cada uno si los cuadernos cuestan los mismo que dos chocolates?
- Matías y su hermano tienen 36 monedas de $5.00 de colección. Si Matias tiene 8 monedas menos que su hermano, ¿cuántas monedas tiene cada uno?
- Gabriela compró, en alguna ocasión, 8 tortas y 5 jugos por los que pagó $152.00 y recuerda que las tortas cuestan $6.00 más que los jugos. ¿Qué pecio tiene una torta y un jugo?
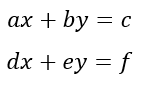










Comentarios
Publicar un comentario