Orden y ubicación de números decimales y fraccionarios

Aprendizaje previo: Conversión de fracciones a decimales y viceversa

Ubico números decimales y fraccionarios en una recta numérica

Para ubicar fracciones en la recta numérica: 
Por ejemplo, ubicar 2/4 

1. Se localiza el cero y los demás números enteros (1, 2, 3, 4, ...)
   
2. Se divide el espacio entre cero y uno en segmentos iguales como indica el denominador. El denominador es 4, por lo tanto se divide en 4.
   
3. Se toman tantas partes como indica el numerador. El numerador es 2, por lo tanto tomamos 2 partes. 
   
4. Ahí se ubica la fracción.
   

Siguiendo la metodología anterior, tenemos el siguiente ejemplo: ubicar 7/2

Podemos convertir la fracción impropia a mixta y tenemos 3 enteros 1/2, por lo tanto la ubicación se encuentra entre el entero 3 y 4, observa:

Fracciones entre dos fracciones dadas

Ejemplo: ubicar una fracción entre 3/5 y 6/5

1. Al tener el mismo denominador, nos basamos en el numerador para ubicar alguna fracción entre estas 
   
2. Entonces podemos encontrar varias fracciones, entre las cuales se encuentran las siguientes: 
   

Ubicar alguna fracción entre 3/4 y 7/6

1. Para ubicar de manera fácil alguna fracción entre esas dos, convertimos al mismo denominador ambas fracciones, entonces tenemos que...
   
2. y al ubicarlos en una recta, lo tenemos de la siguiente manera: 
   
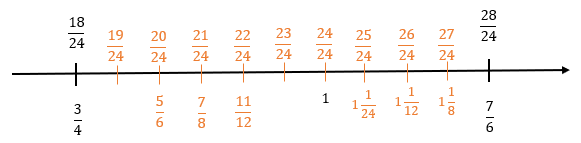
3. A partir de las fracciones anteriores podemos decir que se encuentran las fracciones del 19/24 hasta 27/24 por lo tanto dividimos el segmento de recta de la siguiente manera: 
   
4. Por lo tanto entre la fracción 3/4 y 7/6 podemos encontrar las siguientes fracciones: 
   

Para ubicar decimales en la recta numérica...

Por ejemplo, ubicar 1.9:

1. Se localiza el cero y los demás números enteros (1, 2, 3, 4, ... ) 
   
2. Del número decimal 1.9 se encuentra entre el entero 1 y 2, por lo tanto vamos a dividir  en 10 ese segmento de recta de la siguiente manera:
   
3. A partir de ello, empezamos a ubicar el número solicitado (1.9): 
   

Ubicar algún número decimal entre 1.5 y 1.6

1. Ubicar los números enteros en la recta numérica: 
   
2. Se entiende que los números decimales 1.5 y 1.6 se encuentran entre los enteros 1 y 2, por lo tanto ubicaremos los números de la siguiente manera: 
   
3. Al observar el esquema anterior se puede apreciar que entre el decimal 1.5 y 1.6 es reducido el espacio, pero aun se puede dividir ese segmento de la siguiente manera:
   
4.  Por lo tanto podemos encontrar los siguientes números entre 1.5 y 1.6: 
   
5. Lo anterior se observa en el siguiente esquema:
   

IMPORTANTE: Las fracciones cumplen la propiedad de densidad porque entre dos fracciones distintas siempre se puede encontrar otra entre ellas. Por ejemplo, 5/8 esta entre 1/2 y 3/4. Y como todo número decimal es igual a una fracción decimal, también se tiene que entre 4.5 y 4.55 hay otro número decimal. 

Orden y comparación de números fraccionarios y decimales

Dado dos números distintos, existe una relación de orden entre ellos, es decir, uno de ellos es mayor o menor que el otro. El símbolo > se lee "mayor que" y el < se lee "menor que". Así por ejemplo, 9 > 0 y 3/4 < 5/2 se leen como, nueve es mayor que cero y tres cuartos es menor que cinco medios.

Por ejemplo, ordena las fracciones 1/4, 3/16, 7/64, 5/32 y 1/8 de forma creciente (menor a mayor). 

1. Todas las fracciones tienen diferente denominador, por lo que es necesario convertir al mismo denominador buscando un mínimo común múltiplo (MCM) y utilizando el método de factores primos: 
   
2. Calcular las fracciones equivalentes de cada una, de tal manera que el denominador sea igual al mínimo común múltiplo anteriormente obtenido (64): 
   
3. Al tener las fracciones con un mismo denominador, únicamente ordenamos de menor a mayor (ascendente) los numeradores de cada uno:
   

Ejemplo: escribe el signo <, > o = según corresponda entre las fracciones 7/8 y 3/4:

1. Convertir al mismo denominador las fracciones y tenemos:
   
2. Y entonces tenemos que, 7/8 es mayor que 3/4:
   

ACTIVIDADES:

Utilizando las explicaciones y ejemplos anteriores, resuelve lo siguiente:

1. Escribe el signo <, > o = según corresponda.
   
2. Indica que número representan los puntos en cada recta numérica. 
   
3. Resuelve los siguientes cuestionamientos.
• ¿Cuántas cifras como mínimo, deben tener los números decimales que están entre 1.12 y 1.13?
• ¿Qué número esta a la mitad de 0.32 y 0.43?
• Escribe una fracción que se encuentre entre 3/5 y 5/6
• Ordena de manera descendente las fracciones: 4/6, 5/9 y 8/11
• Representa en una recta numérica la fracción 8/3.